mfd

The mfd class

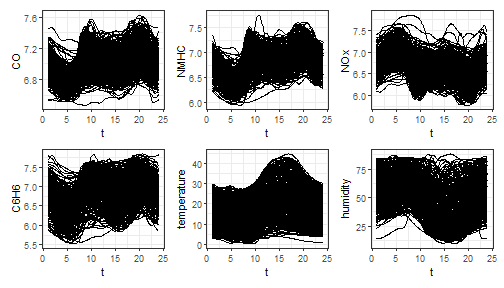
Let us show how the funcharts package works through an example with the dataset air, which has been included from the R package FRegSigCom and is used in the paper of Qi and Luo (2019).

Getting multivariate functional data and the mfd class

We provide the mfd class for multivariate functional data. It inherits from the fd class but provides some additional features:

• It forces the coef argument to be an array even when the number of functional observations and/or the number of functional variables are one
• It provides a better subset function [ that never drops dimensions, then it always returns a mfd object with three-dimensional array argument coef; moreover it allows extracting observations/variables also by name
• When possible, it stores the original raw data in the long data frame format

The first thing is to get the mfd object from discrete data. We currently allow two types of input with the two functions:

1. get_mfd_data.frame: first input must be a data.frame in the long format, with:
   • one arg column giving the argument (x) values,
   • one id column indicating the functional observation,
   • one column per each functional variable indicating the corresponding y values
2. get_mfd_list: first input must be a list of matrices for the case all functional data are observed on the same grid, which:
   • must have all the same dimension,
   • have the variable names as name of the list,
   • are such that, for each matrix:
     • each row corresponds to a functional observation
     • each column corresponds to a point on the grid

In this example, the dataset air is in the second format (list of matrices, with data observed on the same grid)

library(funcharts)
data("air")
fun_covariates <- names(air)[names(air) != "NO2"]
mfdobj_x <- get_mfd_list(air[fun_covariates], grid = 1:24)

Plotting functions

We also provide plotting functions based on ggplot2 and patchwork.

plot_mfd(mfdobj_x)

plot_mfd(mfdobj_x[1:10, c("CO", "C6H6")])